こんにちは。
前回はPythonで粒子フィルタを実装し、状態空間モデルの推定をしました。
今回はその続きとして、状態空間モデルのハイパーパラメータも粒子フィルタで推定できるように改良したいと思います。
・前回の記事はこちら↓
①今回やりたいこと
通常、粒子フィルタを用いた状態空間モデルの推定では、ノイズ分散などのモデル挙動を決めるハイパーパラメータを既知として、状態Xについてのみ逐次推定します。
そのためハイパーパラメータは事前に背景知識やデータから決めておく必要があります。
ⅰ) 状態モデル xt = f(xt-1, v) v:ノイズ ⅱ) 観測モデル yt = g(xt, w) w:ノイズ
しかし、ノイズ分散や、モデル内の係数(例えば線形モデル$Xt=aXt-1+b$の傾き$a$や切片$b$など)など、ハイパーパラメータについてもデータから推定したい場合もあります。
例えば下記のようなシチュエーションです。
・推定対象の系に個体差がある
・測定方法を変更したため、ノイズが減った(増えた)
・データを蓄積・学習することで、さらに予測精度を上げていきたい
状態空間モデルの推定でハイパーパラメータを推定する基本的なアイデアは、
この拡大状態ベクトルについて、逐次推定する方法です。
②状態空間モデルの改良(拡大状態ベクトルの構築)
今回は、前回のランダムウォークモデルにおけるシステムノイズの分散を未知パラメータとします。
拡大状態ベクトルは、考え方は非常に単純です。
前回のモデルに少し手を加えます。
class Transition2:
def __init__(self):
pass
def forcast(self, params):
#標準偏差sigmaでランダムウォークするモデル
#params[0]が位置x
#params[1]がsigma(未知パラメータ)
#sigmaは時間不変とする
params[:,0] = params[:,0] + np.random.normal(0, np.power(10, params[:,1]), params[:,0].shape)
return params
class Observation2:
def __init__(self):
pass
def loglikelihoods(self, params, Yobs):
return norm.logpdf(Yobs, params[:,0], 0.05)前回は各粒子が$x$のみを保持していました。
すなわち、一つ一つの粒子はスカラー値であり、全粒子$(i=1,2,3…N)$の状態$x$をまとめて$N$次元ベクトルparamsとしていました。
今回、各粒子は状態$x$とシステムノイズ$σ$を保持した2次元ベクトルです。
全粒子をまとめたparamsは、2次元ベクトルを$N$個まとめたN×2次元行列となります。
今回:各粒子$(i=1,2,3…N) [xi,σi] → [[x1,σ1],[x2,σ2], [x3,σ], …[xN,σN]]$
③拡大状態ベクトルの推定(普通の粒子フィルターの場合)
さて、構築した状態空間モデルを普通の粒子フィルタで推定してみます。
前回構築した粒子フィルタは下記です。
class ParticleFilter:
def __init__(self, num_particles, dim_param, transition, observation, initial=None):
self.num_particles = num_particles
self.dim_param = dim_param
self.transition = transition
self.observation = observation
if initial is None:
self.particles = np.random.uniform(-2, 2, (num_particles, dim_param))
print('Particles were initialized with uniform distributions.')
elif initial.shape != (num_particles, dim_param):
print('The ”initial” dimension is invalid!')
print('Prease check dimension!')
else:
self.particles = initial
def forcast(self):
self.particles = self.transition.forcast(self.particles)
def filtering(self, Yobs):
loglikelihoods = self.observation.loglikelihoods(self.particles, Yobs)
self.resampling(loglikelihoods)
def resampling(self, loglikelihoods):
#random.choicesのweightは、正規化していないlikelihoodsを直接代入した方が速い
likelihoods = np.exp(loglikelihoods)
idx = np.array(random.choices(np.arange(self.num_particles), weights=likelihoods, k=self.num_particles))
self.particles = self.particles[idx]
キックするコードも前回とほぼ同様です。
pf = ParticleFilter(num_particles=1000,
dim_param=2,
transition=Transition2(),
observation=Observation2()
)
plt.plot(np.arange(0, len(X)), X)
for i, x in enumerate(X):
pf.forcast()
pf.filtering(x)
particles = pf.particles
plt.scatter(np.ones(particles.shape[0])*i, particles[:,0], s=0.1, c='r')
plt.scatter(i, np.mean(particles[:,0]), s=10, c='g')
plt.xlabel('Step')
plt.ylabel('State')
plt.show()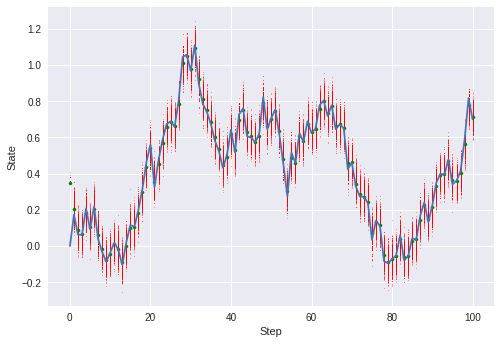
ちゃんと状態推定できているように見えます。
しかしノイズ分散の推定結果はどうでしょう。。。
plt.hist(np.power(10, particles[:,1]))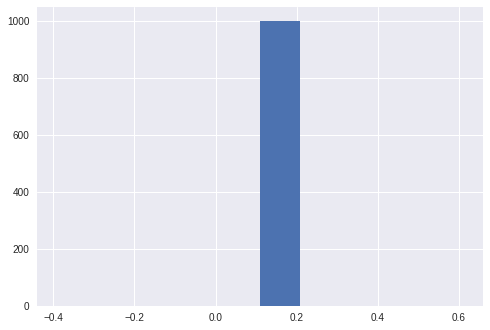
1000個のランダムな値から始めたはずですが、
最終的には全ての粒子が同じ値になっています。
これは「アンサンブルの退化」と呼ばれる現象です。
始めは広がりを持っていたアンサンブルが、リサンプリングを繰り返すうちに、特定の粒子のクローンだけになってしまうために生じます。
こうなってしまうと、アンサンブルで事後分布の形状を表現する粒子フィルターの機能がなくなってしまいます。
これを回避するためには粒子数を増やすのが一つの手ですが、状態ベクトルの次元が大きくなると、必要な粒子数が指数関数的に増えてしまいます。
もう一つの方法が、次に紹介する「融合粒子フィルタ」という手法です。
④融合粒子フィルタ(Merging particle filter)の実装
融合粒子フィルタの詳細は下記の書籍を参照してください。
(楽天ブックスへのリンクになっています。)
融合粒子フィルタは、複数の粒子の重み付き和によって新たな粒子を作成することで、粒子の多様性を低下させにくくする方法です。
普通の粒子フィルタが、個体の選別のみを行う(そのため最終的には一つの個体しか生き残らない)のに対して、
融合粒子フィルタが、個体の選別と交配を行うことで、種の多様性を確保しながら環境に適応するイメージでしょうか。
融合粒子フィルタで肝となる、粒子の重みつき和の決め方は下記論文を参考にしています。
<参考文献>融合粒子フィルタによって推定された浸透解析モデルの有用性の確率論的検証
それでは実装していきます。
前回からの変更点はリサンプリング工程です。
このようなアルゴリズムによって、元の分布形状をできるだけ保持したまま新たなN個のアンサンブルを構成します。
実際のPythonコード例は下記です。
重み付き和の計算部分は、重みパラメータベクトルalphaとの積で計算しています。
class MergingParticleFilter:
def __init__(self, num_particles, dim_param, transition, observation, initial=None):
self.num_particles = num_particles
self.dim_param = dim_param
self.transition = transition
self.observation = observation
self.l = 3
alpha = np.array([3/4, (math.sqrt(13)+1)/8, -(math.sqrt(13)-1)/8])
self.alpha = np.ones((self.dim_param, self.l))*alpha
if initial is None:
self.particles = np.random.uniform(-2, 2, (num_particles, dim_param))
print('Particles were initialized with uniform distributions.')
elif initial.shape != (num_particles, dim_param):
print('The ”initial” dimension is invalid!')
print('Prease check dimension!')
else:
self.particles = initial
def forcast(self):
self.particles = self.transition.forcast(self.particles)
def filtering(self, Yobs):
loglikelihoods = self.observation.loglikelihoods(self.particles, Yobs)
self.resampling(loglikelihoods)
def resampling(self, loglikelihoods):
#random.choicesのweightは、正規化していないlikelihoodsを直接代入した方が速い
likelihoods = np.exp(loglikelihoods)
idx = np.array(random.choices(np.arange(self.num_particles), weights=likelihoods, k=self.num_particles*self.l))
sample = self.particles[idx]
groups = sample.reshape(-1, self.l, self.dim_param)
self.particles = np.sum(groups*self.alpha.T, axis=1)
⑤拡大状態ベクトルの推定(融合粒子フィルタ)
Pythonで実装した融合粒子フィルタクラス(class MergingParticleFilter)を使って、拡大状態ベクトルを推定していきます。
検証には、通常の粒子フィルタの退化がより顕著にわかるように、ステップ数を100→500に増やして検証します。
また、各粒子のパラメータσの分布(ax2)、σのバリエーションの数(ax3)も同時に可視化します。
・通常の粒子フィルタの場合
trans = Transition()
X = np.array([0])
for i in range(500):
X = np.append(X, [trans.forcast(X[-1])], axis=0)
pf = ParticleFilter(num_particles=1000,
dim_param=2,
transition=Transition2(),
observation=Observation2()
)
fig = plt.figure(figsize=(10, 10))
ax1 = fig.add_subplot(311)
ax2 = fig.add_subplot(312)
ax3 = fig.add_subplot(313)
ax1.plot(np.arange(0, len(X)), X)
for i, x in enumerate(X):
pf.forcast()
pf.filtering(x)
particles = pf.particles
ax1.scatter(np.ones(particles.shape[0])*i, particles[:,0], s=0.1, c='r')
ax1.scatter(i, np.mean(particles[:,0]), s=10, c='g')
ax1.set_ylabel('State')
ax2.scatter(np.ones(particles.shape[0])*i, particles[:,1], s=1, c='gray')
ax2.set_ylabel('Log_sigma')
ax3.scatter(i, len(np.unique(particles[:,1])), s=10, c='orange')
ax3.set_yscale('log')
ax3.set_ylabel('Number of unique parameter')
ax3.set_xlabel('Step')
ax3.set_ylim(10**0, 10**4)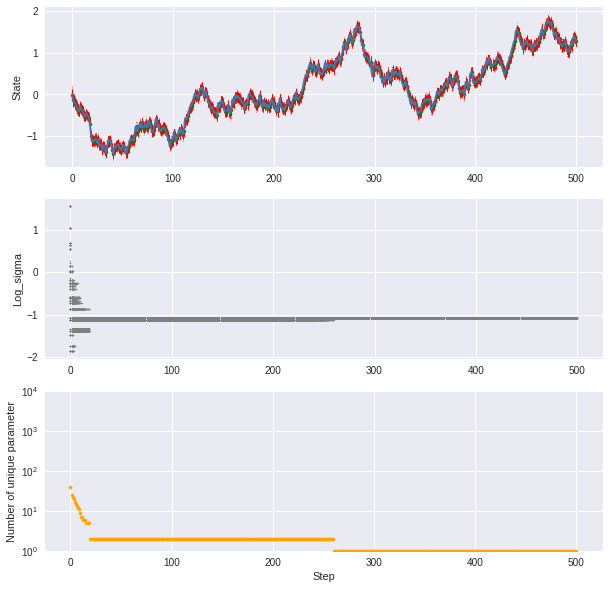
最初は1000個の異なる値を持っていたはずの粒子群ですが、30ステップ目までで殆どが棄却され、260ステップ目付近で実質1種類まで減少してしまいました。
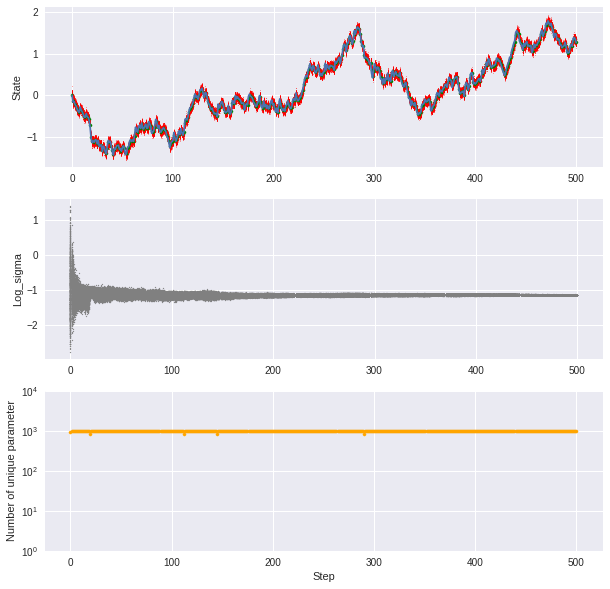
・融合粒子フィルタの場合
mpf = MergingParticleFilter(num_particles=1000,
dim_param=2,
transition=Transition2(),
observation=Observation2()
)
fig = plt.figure(figsize=(10, 10))
ax1 = fig.add_subplot(311)
ax2 = fig.add_subplot(312)
ax3 = fig.add_subplot(313)
ax1.plot(np.arange(0, len(X)), X)
for i, x in enumerate(X):
mpf.forcast()
mpf.filtering(x)
particles = mpf.particles
ax1.scatter(np.ones(particles.shape[0])*i, particles[:,0], s=0.1, c='r')
ax1.scatter(i, np.mean(particles[:,0]), s=10, c='g')
ax1.set_ylabel('State')
ax2.scatter(np.ones(particles.shape[0])*i, particles[:,1], s=1, c='gray')
ax2.set_ylabel('Log_sigma')
ax3.scatter(i, len(np.unique(particles[:,1])), s=10, c='orange')
ax3.set_yscale('log')
ax3.set_ylabel('Number of unique parameter')
ax3.set_xlabel('Step')
ax3.set_ylim(10**0, 10**4)
ステップが進むにつれて、σの予測範囲が絞られてきますが、その中で重みつき和を計算して新たな粒子を生成しているので、粒子の種類は1000種程度をキープしています。
最終的に500ステップ計算後のσの分布をヒストグラムにすると、正規分布の形状を保っており、適切に事後分布を計算できていると見えます。
plt.hist(np.power(10, particles[:,1]))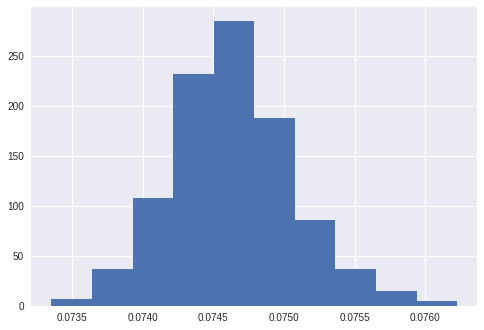
ちなみに事後分布が真値(0.1)よりも小さいのは、観測ノイズを含めずに生成したデータに対して、モデルでは標準偏差0.05の観測ノイズを仮定しているため、システムノイズの推定にバイアスが乗ってしまったためと考えられます。
そもそも本質的に、ランダムウォークのデータに対してシステムノイズと観測ノイズを綺麗に分離するのは難しいと思いますが。
⑥まとめ
今回は、状態空間モデルにおいてハイパーパラメータも含めた拡大状態ベクトルを推定するため、融合粒子フィルタをPythonで実装しました。
状態空間モデルとしては、シンプルなランダムウォークを仮定したため、パラメータ推定しても何が嬉しいのかイメージし難いかもしれません。
しかし状態空間モデルに各々の分野の理論やシミュレーションモデルを当てはめることで、
実データとシミュレーションの合わせ技が使えるようになります。
これはデータ同化(Data assimilation)と呼ばれ、近年は気象学、地球科学等の分野で活用が進んでいる技術です。
特に粒子フィルタは、実装が容易でモデルの自由度が高いため、シミュレーションモデルとの相性が良いです。
私もまだまだ勉強中ですが、データ同化が今の機械学習ブームの次の技術になるのではないかと期待しています。
今回は以上です!
ご参考になれば幸いです。