ベイズ推定で予測の不確実性を計算する【Pythonで実例】

こんにちは。
今回はベイズ推定のメリットの一つ、事後分布で予測の不確かさを表現できるという点を、実際にコードを描きながら見ていきます。

例題としては、回帰分析の問題を設定し、訓練データの多い点、訓練データの少ない点、訓練データのない外挿領域の点について、ガウス過程回帰を用いて予測した場合の事後分布の広がりを見てみます。

〜本日の目次〜

①予測の不確かさを重視する理由
② モデル精度評価では不十分（知りたいのは予測値の確からしさ）
③ 予測しやすいデータと予測が難しいデータの例
④ ガウス過程回帰で予測値の不確かさを求める
⑤ まとめ

①予測の不確かさを重視する理由

近年、機械学習が普及するとともに、幅広い分野でデータ駆動型の研究が盛んです。
例えば、
・最適な実験条件を少ないデータから予測する
・大量データ、高次元データを解析、分類する
などがよくあるタスクでしょうか。
これらのタスクではモデルの精度、つまり正解率を上げることが重要です。（当然と言えば当然）

一方で、製品の耐用年数、安全性の予測など、信頼性が求められる分野への機械学習の適用は成功事例が少ないという実感があります。
その理由の一つは、「その予測値は信頼できるのか？」ということがわかりにくく、意思決定に活用しにくいためです。

例えば機械学習が、「その製品の耐用年数は１０年（予測中央値）」と予測したとして、
「９年〜１１年」なのか
「５年〜１５年」なのか
つまり予測に自信があるかどうかによって、その後のアクションは変わってきます。

製造メーカーであれば、何年補償で販売するか、リース、サブスクリプションなどのビジネスであれば、料金設定をどの程度に設定するか、といった問題です。

重要なのは、予測の幅が大きい（精度が低い）ことではなく、

予測の幅が判らないと、重要な意思決定の場面で取るべきリスクを取れない

という点です。

② モデル精度評価では不十分（知りたいのは予測値の確からしさ）

このような予測の信頼性への問いに対して、例えば交差検定などをおこない、モデルの精度（訓練データに対する平均的な予測誤差）を$RME$ や、$R^2$などを評価する場合も多いように思います。
しかし、モデルの精度指標は、「さまざまなデータ点で検証した結果、平均的な予測のズレはこの程度」といった趣旨の評価指標です。
ざっくりとした解釈としては、過去の問題に対する平均点と言っても良いかもしれません。

一方で、予測に信頼性が求められる状況とは、
予測が（悪い方に）間違えると損害が大きいような状況
です。

この状況で大事なのは過去の平均点ではなくて、目の前の問題に対して確信を持って答えられるかどうかです。

モデル精度のみで予測を信用するというのは、自動車の運転で例えるなら
視界が悪い道なのに、「今まで事故を起こしたことないから大丈夫！」なんて言ってアクセル全開するようなものです。
視界が悪いなら、慎重に運転すべきですよね。

③ 予測しやすいデータと予測が難しいデータの例

ここからは、サンプルデータとして入力xが２次元、出力yが１次元のデータを生成し、データの多い領域、データの少ない領域、データのない外挿領域について、実際に予測がどの程度不確かになるか見ていきます。

例題として、三角関数をベースに生成した二次元曲面（グリッドで表示）からランダムに得られた５０点のサンプルを図示します。
なおサンプルには適当な正規分布に従うノイズを乗せています。

[Python code]

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import seaborn as sns
import pystan

def func(x1, x2):
    w = [0.5, 5.0, 1.0, 5.0]
    y = np.sin(w[0]*x1)+np.cos(w[1]*x1) + np.sin(w[2]*x2)+np.cos(w[3]*x2)
    return y

#真値：メッシュグリッド
x = np.linspace(-1, 1, 20)
X1, X2 = np.meshgrid(x, x)
Y  = func(X1, X2)

#サンプル：プロット
np.random.seed(seed=123)
x1 = np.random.rand(50)*2-1
x2 = np.random.rand(50)*2-1
y = func(x1,x2) + np.random.normal(0, 0.05, len(x1))

#３次元プロットの描写
fig = plt.figure(figsize=(20,10))
ax = fig.add_subplot(projection='3d')
ax.scatter(x1, x2, y, c='r', s=50)
ax.plot_wireframe(X1, X2, Y)
ax.set_xlabel('X1', fontsize=16)
ax.set_ylabel('X2', fontsize=16)
ax.set_zlabel('Y', fontsize=16)
plt.show()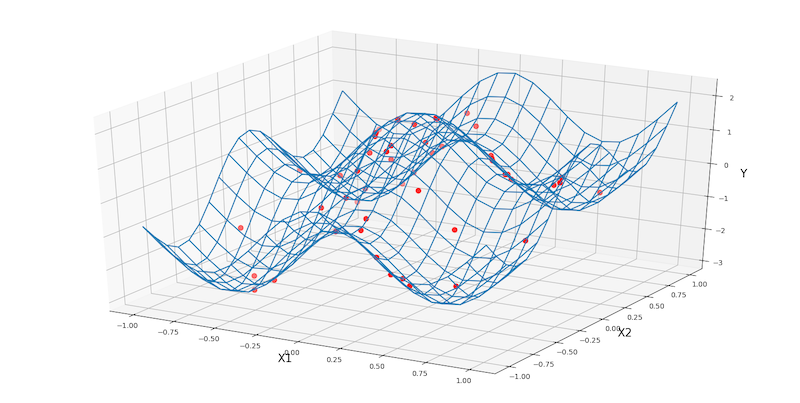

Y軸方向から見た図も示します。

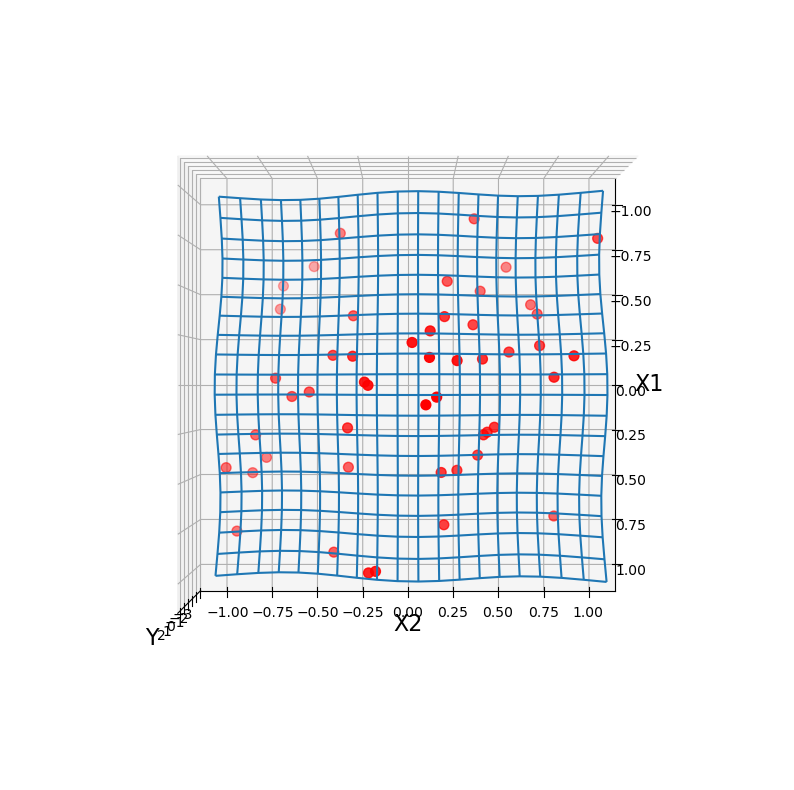
ランダムにサンプリングした５０点のため、データの密度には偏りがみられます。
予測の検証用に、内挿領域で適当に４点（No.0~3）と外挿領域に１点（No.4）のプロットを置きます。
グレーで示した５０個のサンプルを訓練データとして、新たに設定したNo.0~4のy値を予測できるか考えていきます。

x_pred = np.array([[-0.8, 0.0], [0.8, 0.0], [0.0, -0.8], [0.0, 0.8], [1.0, 1.0]])
color = ['blue', 'green', 'red', 'darkviolet', 'orange']

fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(projection='3d')
ax.scatter(x1, x2, y, c='gray', s=50, label='data')
for i in range(5):
    ax.scatter(x_pred[i][0], x_pred[i][1], func(x_pred[i][0], x_pred[i][1]), label = str(i), s = 100, c=color[i])
ax.legend()
ax.plot_wireframe(X1, X2, Y)
ax.set_xlabel('X1', fontsize=16)
ax.set_ylabel('X2', fontsize=16)
ax.set_zlabel('Y', fontsize=16)
ax.view_init(90,0)
plt.show()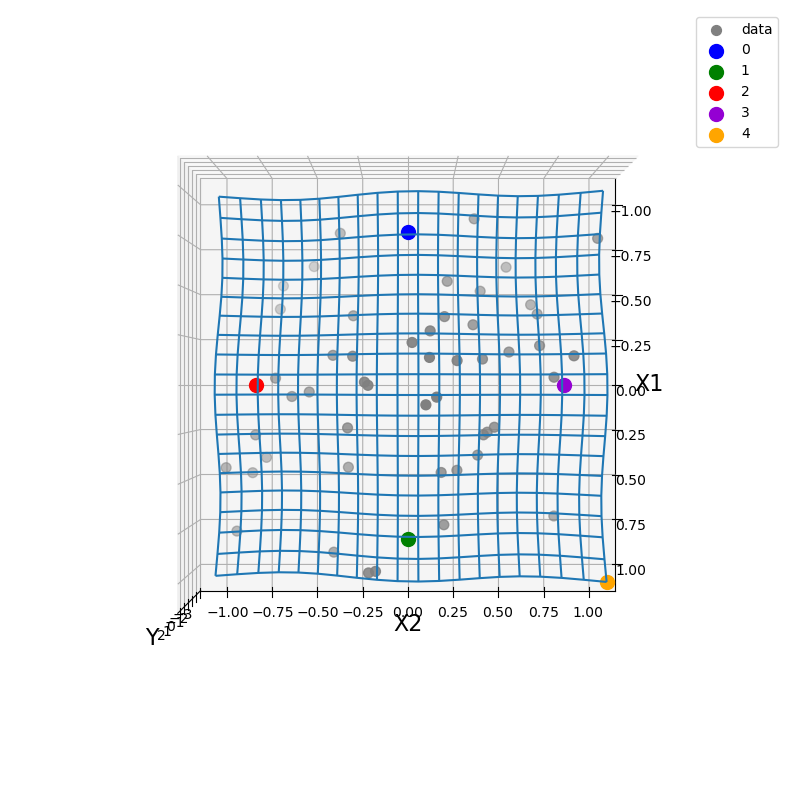

感覚的には、訓練データが近くにあるNo.2、No.3は簡単に予測できそうです。
近くの訓練データと近い値になるだろう、と予想できますよね。
一方でNo.0は内挿領域ではあるものの、訓練データが少ないエリアのため予測が難しそうです。
No.1は、No.2、No.3とNo.0の中間くらいの難易度でしょうか？
No.4は外挿領域であり、訓練データからも離れています。
予測をしようにも根拠がなく、確証のある予測は期待できません。

④ ガウス過程回帰で予測値の不確かさを求める

○モデル

予測モデルとしては、前回ボストン住宅価格データの予測に使ったのと同じ、ガウス過程を使います。
カーネル関数にはRBFカーネルを使い、コードは全く同じです。

【ベイズ推定】Stanでガウス過程回帰

Stanを使ってガウス過程回帰モデルを実装しました。曲線を出力できる柔軟性を持ちつつも、ベイズ推定に基づいてデータの不確かさを考慮できるためオーバーフィッティングをある程度防いでくれるという、非常に使い勝手の良いモデルです。

○サンプリング実行

Stanにデータを渡してMCMCでサンプリングを行ます。
図は非常にわかりにくいですが、ちゃんと収束したようです。

stan_data = {
    "N1":x_data.shape[0],
    "D":x_data.shape[1],
    "x1":x_data,
    "y1":y,
    "N2":x_pred.shape[0],
    "x2":x_pred
}

fit = sm.sampling(data = stan_data, iter=3000, warmup=1000, chains=5)

import matplotlib as mpl
mpl.rcParams['font.size'] = 6
fit.plot()
plt.tight_layout()
plt.show()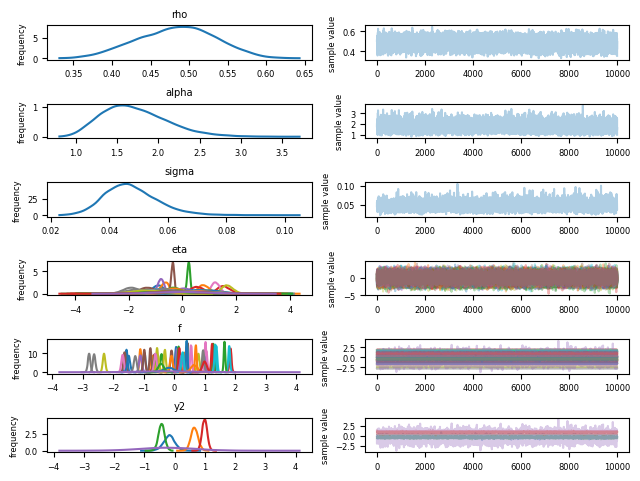

○予測結果の図示

y2の事後分布を図示していきます。
MCMCで得られたサンプルをそのままヒストグラムにしても良いのですが、
seabornのkdeplot()でカーネル法を用いた滑らかな確率密度関数として図示しました。

plt.style.use('seaborn')
fig = plt.figure(figsize=(10,12))

for i in range(5):
    ax = fig.add_subplot(5,1,int(i+1))
    sns.kdeplot(fit.extract()['y2'][:,i], ax=ax, fill = True, label='Posterior', color = color[i])
    ax.axvline(x=func(x_pred[i][0], x_pred[i][1]), ymin=0, ymax=5.0, c = 'black', label = 'True value')
    plt.title('No.'+str(i))
    ax.set_xlabel('y2 value')
    ax.set_xlim(-2.0, 2.0)
    ax.set_ylim(0, 5.0)
    plt.legend()
plt.tight_layout()
plt.show()

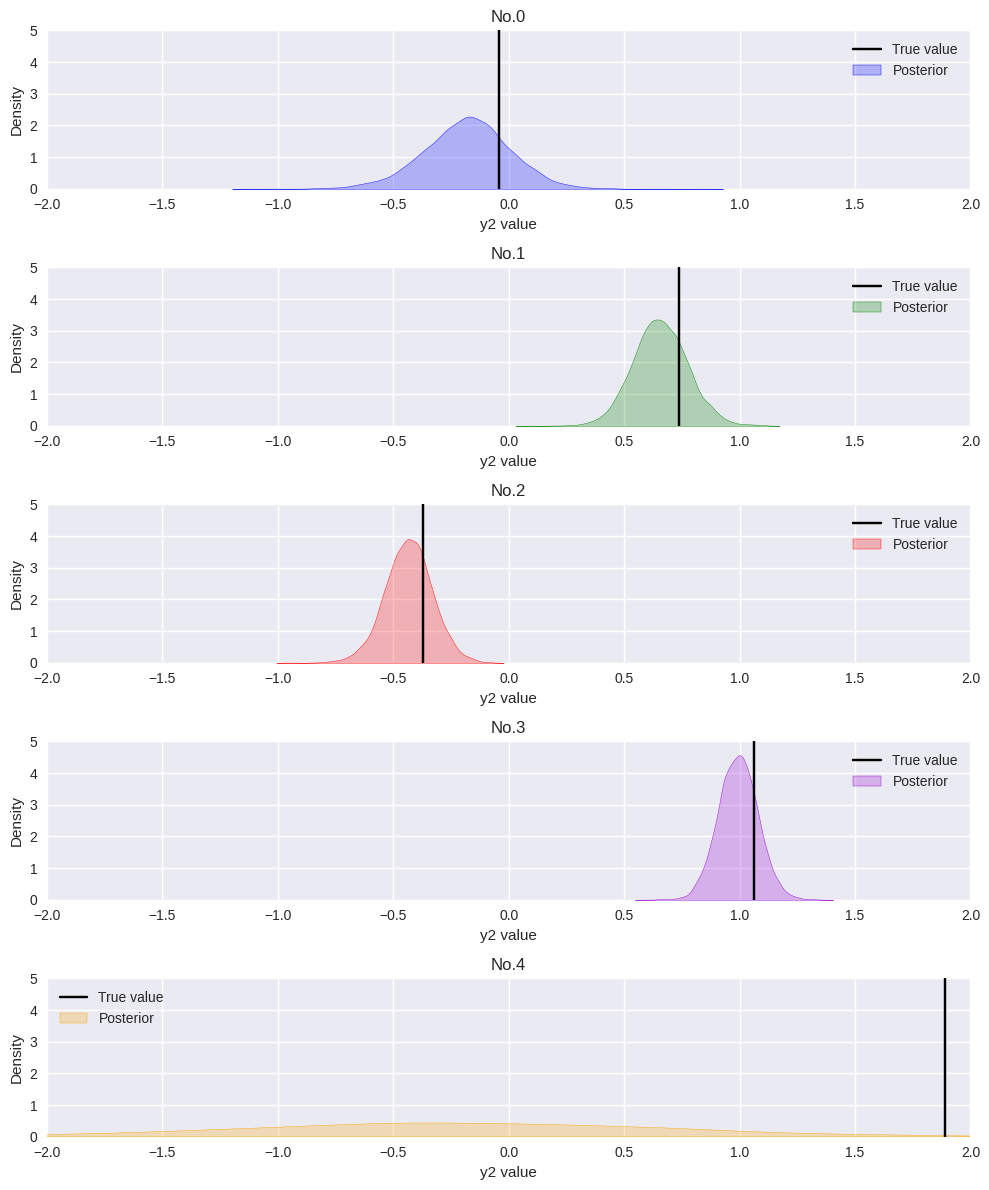
事後分布の広がりを見ると、訓練データが近くにあるNo.2、No.3と比べ、No.0の事後分布が大きく広がっています。
始めにデータの偏りから予想した通り、訓練データが近くに少ないNo.0は、No.2、3と比べて予測の不確かさが大きくなることを上手く表現できているようです。

また外挿領域を無理に推定しようとしたNo.4は分布の広がりが非常に大きくなっています。
「予測の根拠となる訓練データがないので、予測できない！」ということが表現できています。