こんにちは。
今回は私が研究でよく活用しているベイズ推定について解説します。
ベイズ推定って非常にわかりにくいですよね。
ネットで検索しても書いてあることがまちまちで、「結局どんな方法なのかわかりにくい!」と感じる人が多いのではないでしょうか?
わかりにくい原因の一つは、ベイズ推定が「どんな方法か?」と、「何ができるのか?」がごちゃ混ぜになっているためです。
よく見かける解説ですが、主観確率はベイズ推定の特徴の説明ではありません。
主観確率を使うことは必須ではないからです。
「主観確率も、使おうと思えば使える」が正しいです。
・本や解説記事を読んだけど、いまいち飲み込めない…
・人に説明できなくて困っている!
今回はこのような人に向けて、ベイズ推定についてざっくり噛み砕いて解説します。
(必ずしも学術的な正確さを重視しているわけではないので、ご注意ください。)
①ベイズ推定とは?
ベイズ推定を一言で表現すると、「パラメータθを確率変数として考える推定方法」です。
例えば、ある学校の生徒の平均身長を、ある10人分の身長データから推定するとき、現時点でのその学校の生徒の平均身長は、当然ですが確定した値があるはずです。
1000人の学校であれば1000人の身長データが手元にあるかどうかは別として、すでに存在する1000人ですから、平均値として何らかの確定した値があるはずです。
しかし、ベイズ推定の立場では、この平均身長θを確率変数として考えます。平均身長θを不確定な値とするわけです。

自然な考えにも思えますが、伝統的統計学の立場では、θは確定した値なのだから、確率変数として考えるのはおかしいことです。
この点で、伝統的統計学とベイズ統計学で立場が別れます。
とはいえ統計学者ではく、データから役に立つ予測、推論をしたいだけの私たちとしては、伝統的統計学とベイズ統計学の対立は重要ではありません。
重要なのは、パラメータθを確率変数として考えると何がいいのか?という点です。この点については後で述べます。
なお、「ベイズモデル」という特定のモデルはありません。
しかしさまざまな機械学習モデルの中にベイズ的考え方に基づいたモデルがあります。
そういう意味でも、統計推定をする際の考え方、立場、作法的なものと考えた方が良いと思います。
ちなみに、固有名詞として「ベイズ」の名前が入った機械学習モデルとして、有名なものでは「ベイズ最適化」があります。
これはガウス過程(ベイズ的なカーネル法)を実験計画の目的に応用した手法です。
ガウス過程は回帰やクラスタリングなどにも使える汎用性の高いモデルです。回帰モデルとしてPythonとStanで実装した例がこちらにあります。

②ベイズ推定のメリット
メリット1:結果(観測データ)から原因(パラメータθ)の逆推論が容易
機械学習の目的は主に、原因から結果を高精度で予測することです。
より具体的には、説明変数Xが入力値として与えられた時の結果Yを予測するために、手持ちのデータからモデル(関数$f$)を作る方法が機械学習です。
しかし関数$f$は必ずしも、データの背後にあるメカニズムに則っているとは限らないため、関数$f$から何かを考察のは大変です。
(説明変数の重要度を数値化する方法や、ディープラーニングの中間層の学習結果からデータの傾向を捉える方法など、方法がないわけではありません。)
一方で、ベイズ推定では、全てのパラメータを確率変数として置き、データの背後にある因果関係をモデルとして記述します。
それをベイズの定理に当てはめることで因果関係を逆転させて、結果(観測データ)から、原因(パラメータ)を逆推論をすることができます。
当然、原因が推定できれば、次に来るであろう結果を予測することもできます。
この、結果から原因を「逆推論」することは、モジュールとして整備された既存の機械学習モデルでは難しく、ベイズ推定の強みといえます。
メリット2:推定したいパラメータθに予備知識を織り込むことが可能
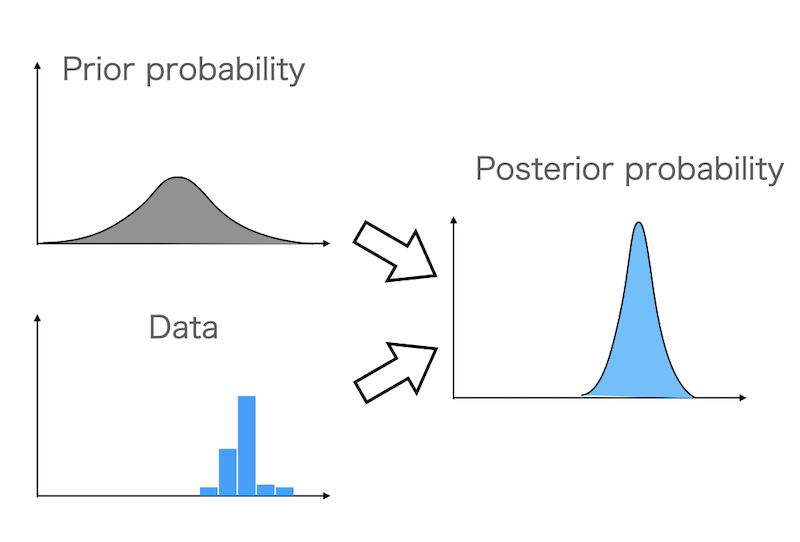
パラメータθに関する予備知識を「事前分布」という形で推論に組み込むことができる点もベイズ推定の強みです。
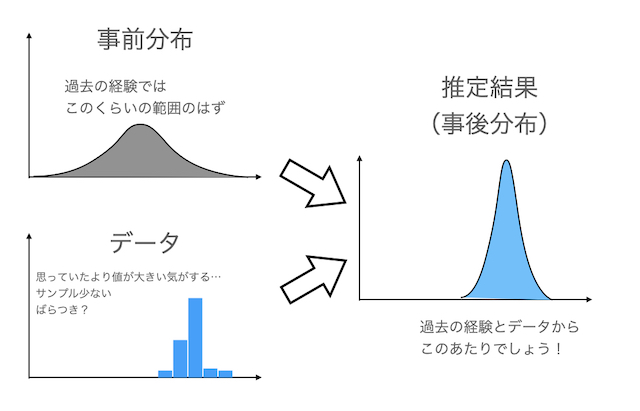
例えば冒頭の平均身長の例でいうと、推定したい生徒と同年齢層の平均身長が既知である場合に、それを考慮できるということです。
10人の身長データだけではサンプルによっては、たまたま平均よりも高い人が多かった時は、当然高めの推定値になります。
しかし、例えば公的データなどから年齢別の平均身長が既知あれば、そのデータを予備知識を使って予測を補正することができます。
予備知識をモデルに組み込むことは決して必須ではなく、正しいかどうかの十分な検討や合意形成が必要です。
しかしそのような予備知識を考慮できるのはベイズ推定にしかないメリットといえます。
ちなみに、事前分布の考え方を応用したのが階層ベイズモデルという手法です。
これは例えば複数の学校の生徒の身長データから、各学校の生徒の平均身長を推定したい場合などに使えます。
各学校で別々に平均値を出しても良いですが、その場合、データの少ない学校に関しては確からしい推定値が求められない、という可能性があります。
ここで、各学校の平均身長は近いはず、という仮定を置くことで、一つ一つの学校のデータは少ないが、他の学校の類似データはある、という場合に類似データも有効活用して効率的に推定をすることができます。
メリット3:推定範囲(確率的な不確実性)を簡単に可視化できる
ベイズ推定は全てのパラメータを確率変数として扱うため、基本的に推定結果は確率分布(あるいは確率分布からサンプリングされた多数の数値群)として得られます。
そのため推定した確率分布をグラフ化するだけで、推定の不確実が可視化できます。
単回帰分析を例にみてみます。
適当なモデル($y=2x-1$ + 正規分布に従うノイズ)から生成したデータに対して、線形回帰モデル(分散は既知)を当てはめました。
推定したモデルの傾きと切片はそれぞれ確率分布に従う多数のサンプルとして得られるので、そのうち代表として推定線を100本引きました。
多数の直線が引かれており、いずれの直線もデータの傾向には概ね適合しています。
今回はイメージを掴むために多数の線で表記しましたが、これを分布、推定区間などで図示することももちろん可能です。
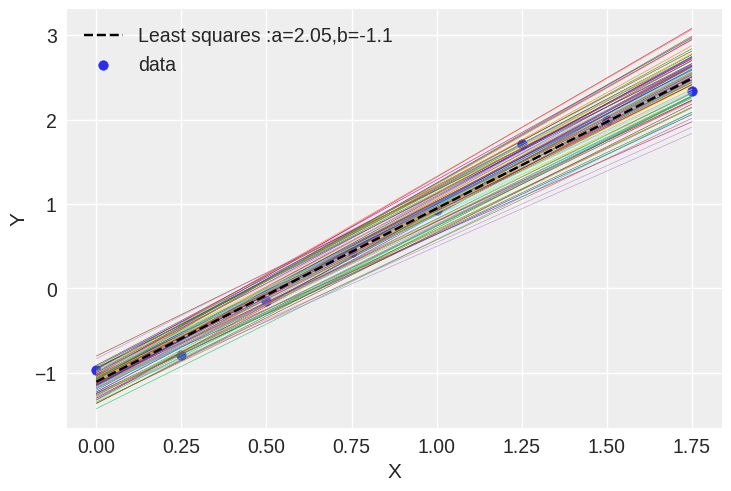
なお、黒破線は最小二乗法で引いた直線です。
最小二乗法では、一本の線がビシッと引かれますが、ベイズ推定を使うと
-
・手持ちのデータに合う直線が複数考えられる
・データを増やせば予測が更新される可能性がある
ということがよくわかります。
ちなみに今回はベイズ推定モデルの測定ノイズは正規分布として表現したため、ベイズ推定結果の中央値をとると、最小二乗法の結果と一致します。
続いて、傾きalphaと切片betaの関係を二次元の等高線としてグラフにします。
黄色の箇所が、確率が高いと推定した値になります。
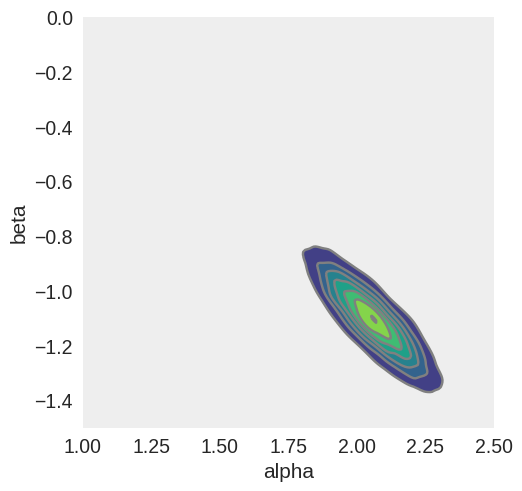
alpha=2.0、beta=-1.0付近に分布の中心があることがわかります。
また、alphaが高いときはbetaが低く、alphaが低いときはbetaが高いことがわかります。
すなわち、少し傾きが緩くて切片が大きい線でも、少し傾きが大きくて切片が小さい線でもデータの傾向には合うということです。
メリット4:データに合わせて解析者がモデルを組み立てることが可能
通常の機械学習的アプローチでは、データに対して幾つかの既存の機械学習モデルを当てはめてみて、既存の中から良いモデルを探すことができます。
一方でベイズ推定は、冒頭にも述べましたが、統計的推定をするにあたっての考え方の一つでしかなく、実際のモデルは解析者がデータに合わせて構築することができます。
既存の機械学習モデルの中から、良いモデルを見つけるようなアプローチ手法(ツールボックスアプローチ)に対して、ベイズ推定のような、データに合わせてモデルを構築する方法を「モデリングアプローチ」と言われることもあるようです。
参考:https://trainz.jp/media/aicareer/23/
③ベイズ推定のデメリット
ここまでメリットばかり紹介してきましたが、もちろんデメリットもあります。
デメリット1:事前分布の設定が難しい

メリット2として予備知識を事前分布として推定に組み込める、と紹介しましたが、この事前分布の設定が難しい、というか非常に奥が深いです。
計算アルゴリズムの進化もあり、解析者がかなり自由に事前分布を設定できます。
しかしこれは諸刃の剣で、極端な事前分布を設定すれば、解析結果もめちゃくちゃになる可能性があります。
先程の回帰分析の例であれば、「傾きは絶対10前後のはずだ!」という事前分布を与えれば、推論結果の傾きも10前後の値になってしまいます。
そのため妥当な推論結果を得るためには、
・出来るだけ客観的な情報のみ事前分布を設定する
・客観的な情報がないときは一様分布などの平坦な分布を設定することで事前情報を与えない
(無情報事前分布)
などに注意する必要があります。
このような性質のため、伝統的な統計手法(たとえばp検定)と比較すると、客観性の求められるデータ分析や、公的なデータ分析に用いるには若干ハードルが高いかもしれません。
(とはいえ解析というのは大抵、使うモデルに依存するため、客観性の議論が大変なのはベイズに限ったことではないですが。)
デメリット2:データに合わせて、解析者がモデルを組み立てる必要がある
既存の機械学習モデルの場合、既存プログラムコードにデータだけ投入すればある程度動きます。
そのため、scikit-learnのように非常に使いやすい整備されたモジュールが数多くあります。
また、コードを書かずして、GUIの画面操作のみで機械学習モデルを作れるソフトウエアやサービスも出てきています。(企業向けの高額なものも含む。)
それらと比較して、ベイズ推定モデルは、データに合わせて解析者がモデルを構築するため、自動化、テンプレート化が難しい側面があります。
つまり、データや背景知識に合わせて数理モデルを組み立てることができる自由度と引き換えに、数学、統計的な知識や慣れが必要になります。
ただし、既存の機械学習手法の一部にベイズ的な手法、考え方を組み込んだモデルもあり、そのような形で広く薄く、活用されていくのかもしれません。
■まとめ
ここまで、ベイズ推定とはどんな方法で、どんなメリットがあるのかを紹介してきました。
ベイズ推定は、解析者が自分でモデルを書くため、若干敷居が高い面もあります。
しかし、全てのパラメータを確率分布として扱うベイズ推定は、一度理解するとさまざまなモデルを統一的に作ることができるようになり、非常に柔軟性のある手法であることがわかるようになります。
以上、ご参考になれば幸いです!

