【Python】粒子フィルタで状態空間モデルの推定

こんにちは。
今回は粒子フィルタという逐次推論アルゴリズムをPythonで実装します。

時系列データを表現する統計モデルの一つに状態空間モデルがあり、
粒子フィルタは状態空間モデルを推定することができるアルゴリズムの一つです。

状態空間モデルを逐次推定するアルゴリズムとしては、カルマンフィルタが代表的です。
しかしモデルに線形・ガウス分布の制約がかかるため用途によっては使いづらいのがデメリットです。

一方で粒子フィルタは、モデルの制約がなく、実装も容易です。
今回はそのメリットを生かすため、粒子フィルタ部分と状態空間モデル部分を別オブジェクトとして構築することでモデル部分を触りやすくしました。

①粒子フィルタの考え方

まず計算する対象である状態空間モデルですが、これは時間発展する挙動（時系列データ）を２つのステップに分けて表現します。

ⅰ)　時間に伴う変化
ⅱ)　各時点での観測

数式で表現すると下記のようになります。

ⅰ) 状態モデル　xt = f(xt-1, v)	v:ノイズ
ⅱ) 観測モデル　yt = g(xt, w)	w:ノイズ

実務ではそれぞれの分野の背景知識を元にⅰ、ⅱのモデルを考えます。

さて、対象に合わせて自由度高く構築できる状態空間モデルですが、
状態モデルで表現した真の状態（xt）はどのように推定すれば良いのでしょうか？
その一つの方法が粒子フィルタです。

ここでの粒子とはあくまで概念的な呼び方です。
推論対象の状態xの確率分布を多数のサンプル集合で表現しており、
一つ一つのサンプルを「粒子」と呼んでいます。

粒子フィルタのアルゴリズム概要

step4が粒子フィルタの肝です。
step2で得られた予測分布に対して、観測データへの当てはまりの良さ（尤度）に従って粒子を抽出し直すことで、
予測値をいい塩梅で観測値に寄せることができます。
ベイズ推定の事後分布（事前分布と尤度関数の積）を求める操作に対応します。

この(step2)〜(step4)を初期〜時刻tまで繰り返すことで、各時刻における状態xを推定します。

②粒子フィルタの実装（class ParticleFilter）

それではPythonで実装していきます。
実装にあたっては下記の記事等を参考にしました。

＜参考１＞https://www.yasutomo57jp.com/2021/07/22/パーティクルフィルタのpython実装/
＜参考２＞https://qiita.com/kenmatsu4/items/c5232b1499dfd00e877d
＜参考３＞https://qiita.com/Keyskey/items/7da429170a1eba5994c2

粒子フィルタの多数の粒子に対する計算をPythonで素朴にforループで書くと非常に遅いため、
できるだけNumpyなどを使って行列計算で実装しています。

import numpy as np
import random
from scipy.stats import norm
import matplotlib.pyplot as plt
plt.style.use('seaborn')

class ParticleFilter:
    def __init__(self, num_particles,  dim_param, transition, observation, initial=None):
        self.num_particles = num_particles
        self.dim_param = dim_param
        self.transition = transition
        self.observation = observation
        if initial is None:
            self.particles = np.random.uniform(-2, 2, (num_particles, dim_param))
            print('Particles were initialized with uniform distributions.')
        elif initial.shape != (num_particles, dim_param):
            print('The　”initial” dimension is invalid!')
            print('Prease check dimension!')
        else:
            self.particles = initial

    def forcast(self):
        self.particles = self.transition.forcast(self.particles)
        
    def filtering(self, Yobs):
        loglikelihoods = self.observation.loglikelihoods(self.particles, Yobs)
        self.resampling(loglikelihoods)
        
    def resampling(self, loglikelihoods):
        #random.choicesのweightは、正規化していないlikelihoodsを直接代入した方が速い
        likelihoods = np.exp(loglikelihoods)
        idx = np.array(random.choices(np.arange(self.num_particles), weights=likelihoods, k=self.num_particles))
        self.particles = self.particles[idx]
        

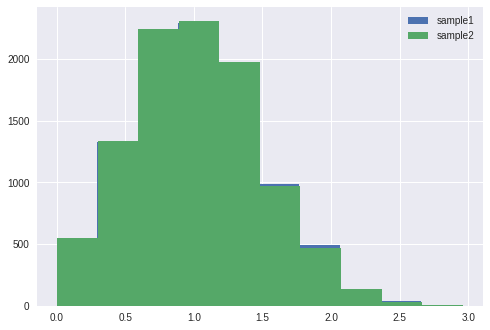
粒子フィルタで重要なリサンプリング部分ですが、Python標準のrandomモジュールを使用しています。

numpyにもランダム復元抽出の関数（numpy.random.choice）があるのですが、
Python標準のrandomモジュールの関数（random.choices）の方が速いです。

また、任意の確率（今回であれば各粒子の尤度）に基づいてサンプリングする際、
確率値は正規化（合計が１となるように）や、累積和にするのが一般的なようです。

しかしPythonで実装する場合には、random.choices内で勝手に処理してくれるので、
余計なことはせずに尤度の値を直接、引数に代入した方が早くなります。
JupyterLab上で実行時間を計測すると倍近い差があります。

num = 10000
x = np.random.uniform(0, 10, num)
likelihoods = norm.pdf(x, 1, 0.5)

%%timeit
cumsum_lh = np.cumsum(likelihoods)/np.sum(likelihoods)
sample2 = random.choices(x, cum_weights=cumsum_lh, k=num)

17.3 ms ± 48.5 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

%%timeit
sample1 = random.choices(x, weights=likelihoods, k=num)

8.91 ms ± 18.8 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)

当然、リサンプリング後の分布形状は同じです。

③状態空間モデルの定義（class Transition, class Observation）

今回は適当に、標準偏差0.1でランダムウォークするモデルとします。
観測モデルは、真値に標準偏差0.05の正規ノイズが乗るとしました。

class Transition:
    def __init__(self):
        pass
    def forcast(self, params):
        #標準偏差0.1でランダムウォークするモデル
        return params + np.random.normal(0, 0.1, params.shape)
    

class Observation:
    def __init__(self):
        pass
    def loglikelihoods(self, params, Yobs):
        return norm.logpdf(Yobs, params, 0.05)

メタ的に、状態モデルから適当なデータを生成しました。

trans = Transition()

X = np.array([0])

for i in range(100):
    X = np.append(X, [trans.forcast(X[-1])], axis=0)

plt.plot(np.arange(0, len(X)), X)
plt.xlabel('Step')
plt.ylabel('State')
plt.show()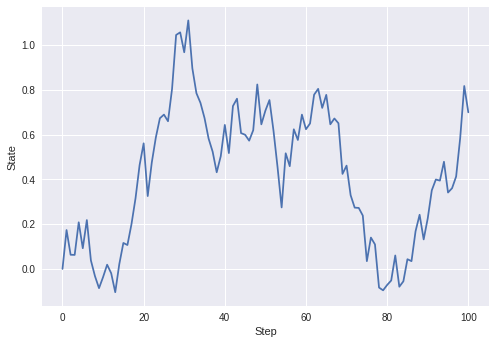

④実行結果

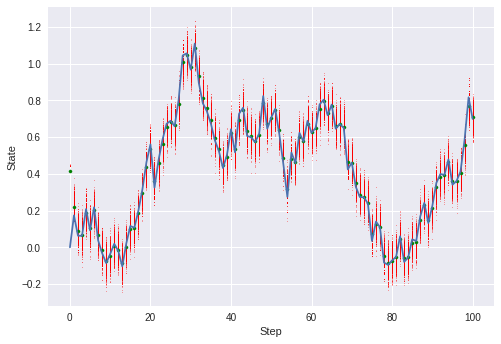
それでは、実装した粒子フィルタを動作させてみます。

今回は粒子数1000でテストしました。
各ステップ毎に、全粒子の位置および平均値を可視化させてみます。

pf = ParticleFilter(num_particles=1000,
                   dim_param=1,
                   transition=Transition(),
                   observation=Observation()
                   )

plt.plot(np.arange(0, len(X)), X)

for i, x in enumerate(X):
    pf.forcast()
    pf.filtering(x)
    particles = pf.particles
    plt.scatter(np.ones(len(particles))*i, particles, s=0.1, c='r')
    plt.scatter(i, np.mean(particles), s=10, c='g')
plt.xlabel('Step')
plt.ylabel('State')
plt.show()

初期値はズレたところ（適当に設定した値）から始まっていますが、
すぐに実測データ（青線）をトレース出来ていることがわかります。

⑤まとめ

今回はPythonで粒子フィルタを実装しました。

今回の書き方は、粒子フィルタのコア部分（class ParticleFilter）と
統計モデルの部分（class Transition, class Observation）が別オブジェクトになっているので、
モデルの検討・修正が容易で、さまざまな時系列データに対して粒子フィルタが適用できると思います。

また、リサンプリングの高速化にもトライしました。

次回は、内部パラメータ（標準偏差）も推論する方法を実装したいと思います。

今回は以上です！
ご参考になれば幸いです。