
こんにちは。電池研究のかたわら、ベイズ統計やPythonの勉強をしています。
今回もStanを使ったベイズ推定モデルを書いていきます。本日はガウス過程回帰モデルを実装します。
ガウス過程に関する詳細な説明は書籍やサイトがすでにあるので省きますが、ざっくりとした理解として、ベイズ統計に基づくカーネル法の一種で、曲線の形(関数)を明示しなくてもデータに適合する丁度よい曲線(の確率分布)を出力するモデルです。
曲線を出力できる柔軟性を持ちつつも、ベイズ推定に基づいてデータの不確かさを考慮できるためオーバーフィッティングをある程度防いでくれるという、非常に使い勝手の良いモデルです。
ガウス過程をより簡単に実装できるPythonライブラリ(GPyなど)もありますが、ここでは、将来的に自由なアレンジが効きそうなStanで地道に実装してみます。
①データセット【ボストン住宅価格データ】
検証に使うデータとしては、Scikit-learnで用意されているボストン住宅価格データを使います。このデータは、目的変数:住宅価格に対して、説明変数:部屋数や立地に関する情報 13種が用意されており、回帰をタスクとした機械学習のチュートリアルとしてよく用いられているデータセットです。各説明変数に関する説明は、Scikit-learnの公式ページ(https://scikit-learn.org/stable/datasets/toy_dataset.html#boston-dataset)を参照してください。
Scikit-learnからインポートしていきます。なお、Bostonデータは500件以上あり、普通のPC環境でガウス過程モデルで計算するのは少々しんどいので、最初の100件のみを使っていきます。
通常、ガウス過程の計算コストは、サンプル数のNに対して、メモリ消費量は $N^2$オーダー、演算量は$N^3$オーダーで増えていきます。
なお、最も計算コストがかかるのは、出力yの共分散行列に関わる部分のため、入力である説明変数の次元が増える分には、計算コストに大きな違いはありません。Stanでは使えませんが、補助変数法という計算コスト削減手法を使う場合は、入力の次元が増えると計算コストは増えるらしいです。(勉強中)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import pystan
from sklearn.datasets import load_boston
#データセットの読み込み
boston = load_boston()
#ターゲット(住宅価格)と特徴量をデータフレームとして結合
df_boston = pd.DataFrame(boston.data, columns = boston.feature_names)
df_boston = df_boston.assign(MEDV = boston.target)
df_boston = df_boston.iloc[0:100]
df_boston.head()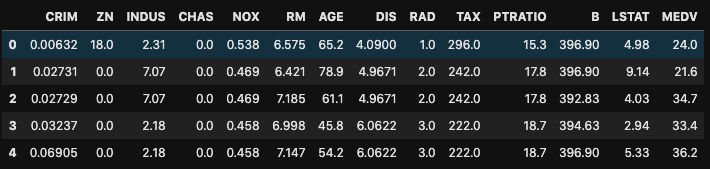
次に生データの傾向を確認していきます。
今回のように、データ系列の数が多い場合、すべての系列の組み合わせについて、散布図をゼロから書くのはしんどいのですが、seabornライブラリのpairplot()関数で散布図行列を描くと簡単にデータの傾向を視覚化できます。
さすがに14系列(説明変数13種+目的変数1種)もあると処理が重ためですが、描いた散布図行列を示しておきます。
import seaborn as sns
sns.pairplot(df_boston)
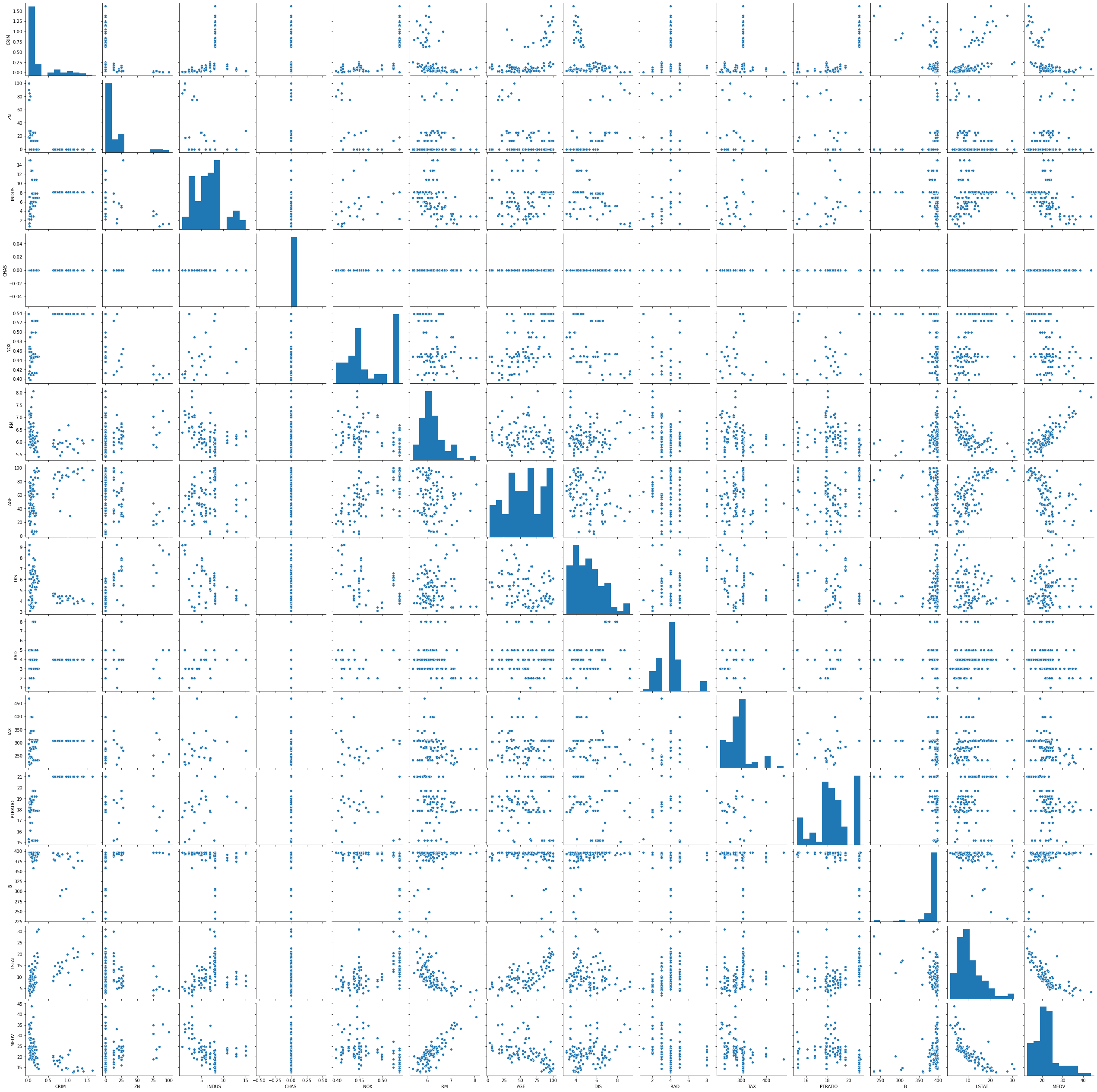
最下段が縦軸:MEDV(住宅価格)と横軸:各説明変数、の散布図です。特にRM(1住宅当たりの平均部屋数)やLSTAT(lower status of the population:高等教育を受けていない成人の割合のことを指すようです。)が住宅価格と相関が強そうです。RMとLSTATとの間にも相関がある点には注意する必要がありそうです。低所得層が多い地域には部屋数が少ない、手頃な家が多いということでしょうか??
②データの標準化
通常、ガウス過程でモデリングする場合、データを予め平均0、分散1に線形変換します。分散1とすることで、ばらつきの大きなデータも小さなデータでもパラメータの探索範囲がしやすくなります。また、平均0とすることで、ガウス過程の定義である、
\begin{eqnarray} f 〜 Normal(μ, \bf{K}\rm)\end{eqnarray}
における平均ベクトルμが0ベクトルとなり、モデル化する必要がなくなります。
今回は、説明変数、目的変数をまとめて、Scikit-learnの関数StandardScaler()で標準化してしまいます。
#ガウス過程でモデリングための前処理として標準化しておく
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
boston_std = sc.fit_transform(df_boston)#出力はnumpy配列
③入力D次元、出力1次元のガウス過程回帰モデル
基本的なStanモデルは、Stanマニュアルに記載があるので、今回はそのまま使います。
なお、ガウス過程では基本的に、未知のプロット$x2$に関する予測値$y2$を得るには、既知のプロット$(x1, y1)$と未知の$(x2, y2)$を合わせた大きな行列$(X, Y)$を作り、$Y$の中の未知パラメータ$y2$の部分を推論する形で予測を行います。(この計算を解析的に分解し、$(x2, y2)$に関わる部分を後で計算する高度な実装方法もあります。
予測したい点数が多い場合は、分解した実装方法が計算コストの観点からおすすめです。)
stan_model = """
data {
int N1;
int D;
vector[D] x1[N1];
vector[N1] y1;
int N2;
vector[D] x2[N2];
}
transformed data {
real delta = 1e-9;
int N = N1 + N2;
vector[D] x[N];
for (n1 in 1:N1) x[n1] = x1[n1];
for (n2 in 1:N2) x[N1 + n2] = x2[n2];
}
parameters {
real rho;
real alpha;
real sigma;
vector[N] eta;
}
transformed parameters {
vector[N] f;
{
matrix[N, N] L_K;
matrix[N, N] K = cov_exp_quad(x, alpha, rho);
// diagonal elements
for (n in 1:N)
K[n, n] = K[n, n] + delta;
L_K = cholesky_decompose(K);
f = L_K * eta;
}
}
model {
rho ~ inv_gamma(5, 5);
alpha ~ normal(0, 1);
sigma ~ normal(0, 1);
eta ~ normal(0, 1);
y1 ~ normal(f[1:N1], sigma);
}
generated quantities {
vector[N2] y2;
for (n2 in 1:N2)
y2[n2] = normal_rng(f[N1 + n2], sigma);
}
""" sm = pystan.StanModel(model_code=stan_model)④予測精度の検証:y-yプロット、線形Ridge回帰モデルとの比較
○フィッティング結果
①でBostonデータから抜き出した100サンプルのデータの内、25サンプル(25%)を精度検証用として、説明変数のみモデルに入力して、住宅価格$\hat{y}2$を予測させてみます。
訓練データと検証データの分割は、Scikit-learnのtrain_test_split()を使いました。
from sklearn.model_selection import train_test_split
train, test = train_test_split(boston_std, test_size = 0.25)
stan_data = {
"N1":train.shape[0],
"D":train.shape[1]-1,
"x1":train[:,0:-1],
"y1":train[:,-1],
"N2":test.shape[0],
"x2":test[:,0:-1]
}
fit = sm.sampling(data = stan_data, iter=3000, warmup=500, chains=3)
フィッティング結果は下記のようになりました。計算の収束を示すRhatがすべて1.0であり、計算が収束したことがわかります。
print(fit)以下は出力結果
Inference for Stan model: anon_model_bf08a6175e5c24a3039caece5ba63a45.
3 chains, each with iter=3000; warmup=500; thin=1;
post-warmup draws per chain=2500, total post-warmup draws=7500.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
rho 5.22 0.02 1.15 3.45 4.4 5.05 5.84 7.95 2137 1.0
alpha 1.33 6.1e-3 0.31 0.87 1.1 1.28 1.49 2.08 2657 1.0
sigma 0.33 6.8e-4 0.04 0.26 0.3 0.33 0.35 0.41 3118 1.0
eta[1] 0.04 2.2e-3 0.16 -0.27 -0.06 0.04 0.14 0.37 5411 1.0
eta[2] 0.99 9.3e-3 0.62 -0.22 0.58 0.99 1.42 2.23 4499 1.0
eta[3] 1.65 6.0e-3 0.36 1.0 1.4 1.63 1.88 2.4 3696 1.0
eta[4] -0.1 3.6e-3 0.26 -0.61 -0.27 -0.1 0.07 0.4 5041 1.0
eta[5] -1.57 5.9e-3 0.31 -2.26 -1.76 -1.55 -1.35 -1.02 2799 1.0
eta[6] -0.45 5.7e-3 0.42 -1.3 -0.73 -0.44 -0.15 0.37 5472 1.0
eta[7] 0.33 5.6e-3 0.39 -0.45 0.07 0.33 0.59 1.09 4912 1.0
eta[8] -1.39 5.6e-3 0.47 -2.34 -1.7 -1.38 -1.08 -0.48 6955 1.0
eta[9] -0.5 7.5e-3 0.54 -1.59 -0.86 -0.49 -0.13 0.55 5261 1.0
eta[10] -0.05 5.1e-3 0.36 -0.77 -0.28 -0.05 0.19 0.68 5022 1.0
eta[11] -2.14 9.6e-3 0.65 -3.41 -2.57 -2.13 -1.7 -0.89 4519 1.0
eta[12] -0.22 7.0e-3 0.71 -1.62 -0.7 -0.23 0.25 1.15 10248 1.0
eta[13] 0.06 8.4e-3 0.82 -1.57 -0.48 0.07 0.61 1.67 9683 1.0
eta[14] -0.18 4.7e-3 0.36 -0.88 -0.41 -0.18 0.05 0.56 5822 1.0
eta[15] -0.53 6.5e-3 0.56 -1.63 -0.91 -0.54 -0.17 0.6 7316 1.0
eta[16] -0.77 6.6e-3 0.5 -1.76 -1.09 -0.76 -0.43 0.16 5609 1.0
eta[17] -0.19 9.2e-3 0.74 -1.68 -0.69 -0.2 0.31 1.26 6553 1.0
eta[18] 0.41 7.4e-3 0.63 -0.82 -0.02 0.41 0.82 1.67 7363 1.0
eta[19] -0.76 7.1e-3 0.66 -2.08 -1.2 -0.76 -0.33 0.53 8530 1.0
eta[20] -0.07 9.1e-3 0.86 -1.76 -0.64 -0.07 0.5 1.62 9008 1.0
eta[21] 0.43 7.1e-3 0.7 -0.98 -0.04 0.43 0.9 1.8 9782 1.0
eta[22] -0.86 0.01 0.95 -2.7 -1.5 -0.84 -0.23 0.98 7160 1.0
eta[23] -0.76 9.5e-3 0.89 -2.48 -1.36 -0.76 -0.16 0.99 8621 1.0
eta[24] 0.27 8.8e-3 0.87 -1.47 -0.31 0.26 0.87 1.94 9740 1.0
eta[25] -0.04 0.01 0.81 -1.6 -0.6 -0.05 0.49 1.62 6485 1.0
eta[26] 0.42 8.9e-3 0.83 -1.19 -0.16 0.43 0.98 2.02 8843 1.0
eta[27] -0.35 8.0e-3 0.79 -1.92 -0.86 -0.36 0.18 1.21 9652 1.0
eta[28] 0.35 8.8e-3 0.88 -1.36 -0.24 0.35 0.94 2.07 9900 1.0
eta[29] -0.2 9.5e-3 0.85 -1.84 -0.78 -0.21 0.37 1.48 7972 1.0
eta[30] 0.3 9.2e-3 0.91 -1.45 -0.32 0.28 0.91 2.12 9915 1.0
eta[31] 1.2 9.5e-3 0.76 -0.29 0.71 1.2 1.71 2.66 6351 1.0
eta[32] -0.17 8.2e-3 0.9 -1.91 -0.77 -0.16 0.43 1.63 11856 1.0
eta[33] 1.36 9.6e-3 0.9 -0.44 0.76 1.37 1.97 3.08 8793 1.0
eta[34] -0.21 8.2e-3 0.75 -1.7 -0.7 -0.22 0.28 1.32 8316 1.0
eta[35] 0.57 9.6e-3 0.93 -1.28 -0.07 0.57 1.19 2.35 9449 1.0
eta[36] -0.45 8.0e-3 0.89 -2.18 -1.05 -0.45 0.15 1.33 12507 1.0
eta[37] -0.96 9.5e-3 0.94 -2.78 -1.6 -0.95 -0.33 0.9 9906 1.0
eta[38] 0.21 10.0e-3 0.92 -1.62 -0.39 0.22 0.81 2.05 8476 1.0
eta[39] -0.44 8.6e-3 0.93 -2.23 -1.07 -0.45 0.19 1.36 11575 1.0
eta[40] -0.01 7.9e-3 0.66 -1.31 -0.46 -0.03 0.42 1.33 6905 1.0
eta[41] -0.22 8.7e-3 0.76 -1.77 -0.73 -0.19 0.3 1.22 7703 1.0
eta[42] -0.43 9.2e-3 0.92 -2.23 -1.06 -0.45 0.18 1.39 10098 1.0
eta[43] -0.15 9.8e-3 0.92 -2.0 -0.77 -0.13 0.48 1.62 8925 1.0
eta[44] -0.02 9.2e-3 0.86 -1.7 -0.6 -0.04 0.54 1.71 8804 1.0
eta[45] -0.08 8.5e-3 0.97 -2.02 -0.72 -0.07 0.57 1.82 12952 1.0
eta[46] -0.15 8.6e-3 0.93 -1.91 -0.77 -0.16 0.48 1.66 11691 1.0
eta[47] -0.05 8.8e-3 0.99 -1.98 -0.7 -0.05 0.59 1.88 12484 1.0
eta[48] -0.1 8.4e-3 0.94 -1.97 -0.73 -0.1 0.52 1.7 12463 1.0
eta[49] -0.26 8.9e-3 0.97 -2.18 -0.91 -0.28 0.4 1.65 11838 1.0
eta[50] 0.01 9.1e-3 0.97 -1.89 -0.65 0.02 0.68 1.89 11367 1.0
eta[51] -0.09 9.7e-3 0.97 -1.99 -0.73 -0.1 0.56 1.83 9945 1.0
eta[52] 0.18 0.01 0.98 -1.72 -0.49 0.19 0.84 2.06 8815 1.0
eta[53] -0.14 9.2e-3 0.94 -1.97 -0.77 -0.14 0.49 1.74 10471 1.0
eta[54] -0.15 8.8e-3 0.94 -1.97 -0.78 -0.16 0.47 1.68 11441 1.0
eta[55] 0.07 9.0e-3 0.95 -1.78 -0.57 0.08 0.73 1.87 11001 1.0
eta[56] 0.05 0.01 1.0 -1.94 -0.61 0.04 0.71 2.05 9060 1.0
eta[57] -0.52 9.6e-3 0.98 -2.47 -1.17 -0.52 0.13 1.41 10382 1.0
eta[58] 0.11 9.4e-3 0.99 -1.86 -0.56 0.11 0.79 2.06 11102 1.0
eta[59] -0.11 9.2e-3 0.96 -2.04 -0.76 -0.11 0.56 1.78 10941 1.0
eta[60] -0.03 9.6e-3 0.99 -1.97 -0.69 -0.02 0.64 1.89 10444 1.0
eta[61] -0.22 9.7e-3 1.0 -2.16 -0.89 -0.21 0.45 1.73 10588 1.0
eta[62] 0.57 8.4e-3 0.83 -1.1 0.02 0.58 1.13 2.19 9775 1.0
eta[63] 0.38 9.3e-3 0.92 -1.45 -0.24 0.38 1.01 2.14 9856 1.0
eta[64] 0.78 9.4e-3 0.83 -0.88 0.23 0.8 1.34 2.37 7700 1.0
eta[65] -0.26 7.6e-3 0.72 -1.65 -0.74 -0.26 0.21 1.16 8972 1.0
eta[66] -0.17 9.9e-3 0.87 -1.87 -0.75 -0.17 0.41 1.54 7780 1.0
eta[67] 0.8 8.1e-3 0.76 -0.75 0.3 0.82 1.31 2.22 8644 1.0
eta[68] -0.07 9.7e-3 0.97 -1.94 -0.72 -0.07 0.59 1.85 9938 1.0
eta[69] -0.05 9.5e-3 1.01 -2.01 -0.75 -0.05 0.65 1.92 11264 1.0
eta[70] -0.01 9.7e-3 0.99 -1.97 -0.69 -0.03 0.64 1.98 10538 1.0
eta[71] -0.17 9.6e-3 0.96 -2.05 -0.83 -0.19 0.49 1.72 10050 1.0
eta[72] 6.3e-3 8.7e-3 0.98 -1.9 -0.65 8.6e-3 0.67 1.94 12883 1.0
eta[73] 0.03 0.01 0.96 -1.84 -0.61 0.04 0.67 1.88 9141 1.0
eta[74] 0.2 8.1e-3 0.81 -1.39 -0.33 0.2 0.74 1.8 9973 1.0
eta[75] 0.07 9.3e-3 0.99 -1.88 -0.59 0.08 0.73 2.04 11464 1.0
eta[76] -0.01 9.7e-3 1.0 -1.95 -0.69-4.5e-3 0.67 1.95 10721 1.0
eta[77] -2.1e-3 8.8e-3 0.98 -1.93 -0.66 1.5e-3 0.65 1.92 12384 1.0
eta[78] -5.6e-3 0.01 1.0 -1.98 -0.68 -0.02 0.66 2.0 9358 1.0
eta[79] 2.6e-3 9.4e-3 1.0 -1.97 -0.67 4.6e-3 0.68 1.93 11398 1.0
eta[80] 0.02 8.9e-3 1.0 -1.95 -0.66 0.03 0.7 1.95 12653 1.0
eta[81] 2.0e-4 9.6e-3 1.0 -1.99 -0.67 3.8e-3 0.66 1.95 10727 1.0
eta[82] -1.3e-3 9.7e-3 0.98 -1.91 -0.66-3.3e-3 0.65 1.91 10109 1.0
eta[83] 1.5e-3 9.5e-3 1.0 -1.96 -0.67 3.9e-3 0.66 2.01 11102 1.0
eta[84] 0.01 9.1e-3 1.0 -1.94 -0.67 0.01 0.72 1.95 12031 1.0
eta[85] 5.3e-4 9.3e-3 1.01 -1.98 -0.7 9.3e-3 0.7 1.96 11901 1.0
eta[86] -0.02 9.1e-3 0.99 -1.97 -0.7-8.0e-3 0.66 1.9 11784 1.0
eta[87] -6.3e-3 8.5e-3 1.01 -1.99 -0.68 -0.01 0.67 1.97 13988 1.0
eta[88] 0.01 10.0e-3 0.99 -1.93 -0.66 0.02 0.69 1.93 9753 1.0
eta[89] 3.4e-3 8.7e-3 1.01 -1.96 -0.68 7.6e-3 0.67 1.99 13475 1.0
eta[90] 0.02 9.8e-3 1.0 -1.93 -0.64 0.02 0.71 1.97 10311 1.0
eta[91] 1.4e-3 9.5e-3 0.99 -1.95 -0.66 0.01 0.67 1.94 10886 1.0
eta[92] 8.5e-3 0.01 1.01 -1.98 -0.67 0.01 0.67 1.99 10049 1.0
eta[93] -0.02 9.4e-3 1.0 -1.96 -0.71 -0.02 0.66 1.95 11267 1.0
eta[94] 1.1e-3 9.5e-3 1.0 -1.97 -0.67 0.01 0.68 1.93 11163 1.0
eta[95] 0.01 10.0e-3 1.0 -1.93 -0.66 7.2e-3 0.69 1.98 9977 1.0
eta[96] -0.03 0.01 1.0 -2.02 -0.69 -0.02 0.62 1.96 9789 1.0
eta[97] -6.3e-3 9.9e-3 1.02 -2.0 -0.7 -0.01 0.68 2.01 10550 1.0
eta[98] -0.02 9.2e-3 1.01 -1.99 -0.71 -0.02 0.65 1.98 12065 1.0
eta[99] -8.6e-3 0.01 0.99 -1.93 -0.69 -0.02 0.68 1.9 9838 1.0
eta[100] 2.8e-3 0.01 0.99 -1.94 -0.66 3.2e-3 0.69 1.91 9270 1.0
f[1] 0.05 2.6e-3 0.2 -0.34 -0.08 0.05 0.18 0.43 5669 1.0
f[2] 0.4 2.5e-3 0.22 -0.04 0.25 0.4 0.55 0.84 8065 1.0
f[3] 1.81 2.4e-3 0.2 1.43 1.68 1.81 1.95 2.21 6571 1.0
f[4] 0.23 2.8e-3 0.21 -0.19 0.09 0.23 0.37 0.64 5751 1.0
f[5] -0.63 1.6e-3 0.15 -0.92 -0.73 -0.63 -0.53 -0.35 8633 1.0
f[6] -0.1 1.6e-3 0.15 -0.4 -0.2 -0.11-5.7e-3 0.19 9336 1.0
f[7] -0.5 3.0e-3 0.27 -1.04 -0.67 -0.5 -0.31 0.03 8068 1.0
f[8] -1.49 2.6e-3 0.25 -1.96 -1.66 -1.49 -1.32 -0.99 9468 1.0
f[9] -0.27 1.9e-3 0.17 -0.6 -0.38 -0.27 -0.16 0.05 7990 1.0
f[10] -0.45 1.8e-3 0.17 -0.78 -0.56 -0.45 -0.33 -0.11 8817 1.0
f[11] 0.8 2.0e-3 0.18 0.44 0.67 0.79 0.92 1.16 8667 1.0
f[12] -1.49 2.6e-3 0.27 -1.99 -1.66 -1.49 -1.31 -0.95 10552 1.0
f[13] -0.43 2.0e-3 0.18 -0.79 -0.55 -0.43 -0.31 -0.08 8344 1.0
f[14] -0.54 3.0e-3 0.3 -1.13 -0.74 -0.54 -0.34 0.06 10205 1.0
f[15] 0.22 2.5e-3 0.19 -0.16 0.1 0.23 0.35 0.59 5831 1.0
f[16] 0.19 1.7e-3 0.16 -0.12 0.08 0.19 0.3 0.51 9581 1.0
f[17] -0.32 1.8e-3 0.17 -0.66 -0.44 -0.32 -0.21 0.02 8840 1.0
f[18] 0.03 2.6e-3 0.24 -0.43 -0.13 0.04 0.19 0.51 8600 1.0
f[19] 0.45 1.7e-3 0.16 0.13 0.34 0.45 0.56 0.75 8683 1.0
f[20] -0.28 1.8e-3 0.18 -0.62 -0.39 -0.28 -0.16 0.07 9531 1.0
f[21] 1.54 2.2e-3 0.2 1.15 1.4 1.53 1.67 1.95 8372 1.0
f[22] -0.39 2.2e-3 0.2 -0.81 -0.53 -0.39 -0.25 3.4e-3 8634 1.0
f[23] -0.39 1.7e-3 0.17 -0.71 -0.5 -0.39 -0.28 -0.07 9394 1.0
f[24] -0.19 1.8e-3 0.17 -0.51 -0.3 -0.19 -0.08 0.15 9045 1.0
f[25] -0.28 1.8e-3 0.17 -0.6 -0.39 -0.28 -0.17 0.05 8916 1.0
f[26] -0.09 1.5e-3 0.15 -0.38 -0.19 -0.09 0.01 0.21 9688 1.0
f[27] -1.26 2.3e-3 0.19 -1.66 -1.39 -1.26 -1.14 -0.88 7376 1.0
f[28] -0.4 2.1e-3 0.2 -0.81 -0.54 -0.4 -0.27-8.9e-3 9409 1.0
f[29] -0.77 1.8e-3 0.17 -1.1 -0.89 -0.78 -0.67 -0.44 8459 1.0
f[30] -0.6 2.0e-3 0.22 -1.03 -0.75 -0.6 -0.45 -0.17 11522 1.0
f[31] 2.68 2.7e-3 0.23 2.22 2.52 2.68 2.83 3.13 7650 1.0
f[32] 0.02 2.1e-3 0.2 -0.37 -0.11 0.02 0.16 0.41 9573 1.0
f[33] 2.96 3.7e-3 0.25 2.47 2.79 2.96 3.12 3.45 4458 1.0
f[34] -1.04 1.3e-3 0.13 -1.29 -1.12 -1.04 -0.95 -0.78 9945 1.0
f[35] -0.42 1.6e-3 0.17 -0.75 -0.53 -0.42 -0.31 -0.09 11841 1.0
f[36] -1.31 1.7e-3 0.16 -1.62 -1.41 -1.31 -1.2 -1.0 9385 1.0
f[37] 0.83 3.2e-3 0.21 0.41 0.69 0.83 0.97 1.23 4307 1.0
f[38] -0.66 1.7e-3 0.15 -0.94 -0.76 -0.66 -0.56 -0.36 7383 1.0
f[39] -1.3 1.9e-3 0.19 -1.67 -1.42 -1.3 -1.17 -0.92 10472 1.0
f[40] 1.07 1.5e-3 0.15 0.78 0.97 1.06 1.17 1.36 10326 1.0
f[41] -0.14 1.8e-3 0.18 -0.49 -0.26 -0.14 -0.02 0.22 9891 1.0
f[42] -0.81 2.1e-3 0.18 -1.17 -0.93 -0.81 -0.69 -0.46 7188 1.0
f[43] -1.11 1.9e-3 0.19 -1.49 -1.24 -1.11 -0.98 -0.75 9828 1.0
f[44] -1.29 3.1e-3 0.28 -1.84 -1.47 -1.29 -1.11 -0.74 8066 1.0
f[45] -0.09 1.5e-3 0.15 -0.38 -0.19 -0.09 4.3e-3 0.19 9346 1.0
f[46] 0.44 2.0e-3 0.17 0.1 0.32 0.44 0.56 0.78 7400 1.0
f[47] 1.31 1.8e-3 0.16 1.0 1.21 1.32 1.42 1.62 7810 1.0
f[48] -0.34 1.6e-3 0.15 -0.64 -0.44 -0.34 -0.24 -0.04 9651 1.0
f[49] -1.03 1.3e-3 0.13 -1.29 -1.12 -1.03 -0.94 -0.77 10315 1.0
f[50] -0.84 1.1e-3 0.11 -1.05 -0.91 -0.84 -0.76 -0.63 8916 1.0
f[51] 1.93 1.9e-3 0.16 1.62 1.82 1.93 2.04 2.25 7257 1.0
f[52] 0.07 1.8e-3 0.17 -0.26 -0.04 0.07 0.18 0.4 9110 1.0
f[53] -1.17 2.1e-3 0.21 -1.58 -1.3 -1.16 -1.03 -0.76 9519 1.0
f[54] 6.6e-3 1.5e-3 0.15 -0.29 -0.09 5.9e-3 0.11 0.3 9684 1.0
f[55] -0.18 2.0e-3 0.18 -0.55 -0.3 -0.18 -0.06 0.18 8355 1.0
f[56] -0.92 1.2e-3 0.11 -1.15 -1.0 -0.92 -0.84 -0.7 8485 1.0
f[57] 1.24 2.1e-3 0.19 0.86 1.12 1.24 1.36 1.6 7834 1.0
f[58] -0.36 1.6e-3 0.15 -0.66 -0.46 -0.36 -0.26 -0.06 9001 1.0
f[59] -1.53 2.0e-3 0.19 -1.91 -1.66 -1.53 -1.4 -1.15 9474 1.0
f[60] -0.3 1.6e-3 0.16 -0.62 -0.41 -0.3 -0.19 0.01 9490 1.0
f[61] 0.39 1.7e-3 0.17 0.06 0.28 0.39 0.5 0.72 9780 1.0
f[62] 1.68 2.9e-3 0.27 1.13 1.49 1.68 1.86 2.2 8905 1.0
f[63] 0.83 2.2e-3 0.23 0.39 0.68 0.83 0.98 1.3 10487 1.0
f[64] 1.94 2.9e-3 0.27 1.41 1.76 1.94 2.12 2.46 8680 1.0
f[65] 0.41 2.9e-3 0.26 -0.1 0.25 0.42 0.59 0.92 8030 1.0
f[66] -0.1 1.8e-3 0.17 -0.43 -0.21 -0.1 0.01 0.22 8267 1.0
f[67] 1.35 3.2e-3 0.29 0.79 1.16 1.35 1.54 1.91 8135 1.0
f[68] 0.05 1.9e-3 0.18 -0.3 -0.07 0.05 0.17 0.4 8953 1.0
f[69] -0.25 1.8e-3 0.18 -0.6 -0.37 -0.25 -0.13 0.11 10008 1.0
f[70] -0.19 1.5e-3 0.14 -0.47 -0.29 -0.19 -0.1 0.09 9525 1.0
f[71] 0.74 2.1e-3 0.17 0.39 0.63 0.75 0.86 1.07 6712 1.0
f[72] 0.43 1.7e-3 0.15 0.13 0.33 0.44 0.53 0.72 8170 1.0
f[73] 0.13 1.3e-3 0.14 -0.14 0.04 0.13 0.22 0.41 11040 1.0
f[74] -0.35 2.7e-3 0.27 -0.88 -0.53 -0.36 -0.17 0.17 10040 1.0
f[75] 0.08 1.8e-3 0.17 -0.26 -0.03 0.08 0.19 0.41 8278 1.0
f[76] 0.46 1.3e-3 0.14 0.18 0.37 0.46 0.55 0.72 11685 1.0
f[77] -0.17 2.5e-3 0.22 -0.61 -0.31 -0.16 -0.02 0.26 7926 1.0
f[78] -0.45 2.9e-3 0.27 -1.01 -0.62 -0.44 -0.27 0.05 8655 1.0
f[79] 0.52 5.5e-3 0.48 -0.48 0.2 0.53 0.85 1.42 7695 1.0
f[80] 0.05 3.5e-3 0.34 -0.64 -0.17 0.06 0.28 0.71 9426 1.0
f[81] 1.84 2.5e-3 0.2 1.45 1.69 1.83 1.97 2.24 6704 1.0
f[82] 0.04 3.0e-3 0.29 -0.54 -0.15 0.04 0.24 0.62 9489 1.0
f[83] -0.31 1.8e-3 0.16 -0.62 -0.42 -0.31 -0.2 0.01 8566 1.0
f[84] -0.24 1.9e-3 0.18 -0.59 -0.36 -0.24 -0.12 0.1 8400 1.0
f[85] 0.11 2.9e-3 0.2 -0.31 -0.02 0.11 0.25 0.5 4915 1.0
f[86] -0.77 3.2e-3 0.32 -1.39 -0.98 -0.77 -0.57 -0.15 9963 1.0
f[87] 0.44 1.2e-3 0.12 0.2 0.36 0.44 0.52 0.69 9537 1.0
f[88] -1.5 2.3e-3 0.23 -1.95 -1.66 -1.51 -1.35 -1.06 9629 1.0
f[89] 0.79 1.3e-3 0.12 0.54 0.71 0.79 0.87 1.03 9115 1.0
f[90] 1.92 4.7e-3 0.42 1.08 1.65 1.92 2.2 2.77 8181 1.0
f[91] -1.4e-3 1.2e-3 0.12 -0.23 -0.08-5.4e-4 0.08 0.23 8969 1.0
f[92] 1.27 2.8e-3 0.28 0.72 1.08 1.27 1.45 1.82 9639 1.0
f[93] -1.43 1.8e-3 0.18 -1.78 -1.55 -1.43 -1.31 -1.1 9733 1.0
f[94] 0.85 5.0e-3 0.5 -0.11 0.53 0.86 1.17 1.82 10050 1.0
f[95] -0.1 3.2e-3 0.29 -0.65 -0.29 -0.1 0.09 0.49 7944 1.0
f[96] -0.61 2.4e-3 0.21 -1.05 -0.75 -0.61 -0.47 -0.21 8179 1.0
f[97] -0.22 3.5e-3 0.35 -0.91 -0.45 -0.22 0.01 0.48 10190 1.0
f[98] 0.06 1.8e-3 0.18 -0.29 -0.06 0.06 0.18 0.42 9536 1.0
f[99] -0.58 2.4e-3 0.23 -1.02 -0.73 -0.59 -0.44 -0.12 8952 1.0
f[100] -0.73 5.2e-3 0.42 -1.52 -1.02 -0.75 -0.47 0.12 6544 1.0
y2[1] 0.46 4.1e-3 0.35 -0.23 0.23 0.46 0.7 1.16 7446 1.0
y2[2] -0.16 4.6e-3 0.4 -0.95 -0.43 -0.16 0.1 0.65 7663 1.0
y2[3] -0.45 4.8e-3 0.43 -1.32 -0.74 -0.45 -0.16 0.39 8085 1.0
y2[4] 0.51 6.8e-3 0.59 -0.65 0.13 0.52 0.92 1.63 7553 1.0
y2[5] 0.06 5.4e-3 0.47 -0.88 -0.26 0.06 0.38 0.98 7702 1.0
y2[6] 1.83 4.7e-3 0.39 1.05 1.57 1.83 2.1 2.6 6994 1.0
y2[7] 0.05 4.9e-3 0.44 -0.8 -0.25 0.05 0.34 0.91 7983 1.0
y2[8] -0.32 4.2e-3 0.37 -1.03 -0.57 -0.31 -0.07 0.4 7458 1.0
y2[9] -0.24 4.4e-3 0.38 -0.99 -0.5 -0.24 0.01 0.5 7266 1.0
y2[10] 0.12 4.8e-3 0.39 -0.63 -0.15 0.11 0.38 0.89 6774 1.0
y2[11] -0.77 5.1e-3 0.46 -1.64 -1.08 -0.77 -0.47 0.13 7906 1.0
y2[12] 0.44 4.0e-3 0.35 -0.25 0.2 0.43 0.67 1.14 7766 1.0
y2[13] -1.5 4.7e-3 0.4 -2.3 -1.77 -1.5 -1.23 -0.73 7415 1.0
y2[14] 0.79 4.0e-3 0.35 0.1 0.55 0.79 1.03 1.48 7817 1.0
y2[15] 1.93 6.0e-3 0.54 0.86 1.57 1.93 2.29 2.98 8166 1.0
y2[16] -6.6e-3 4.2e-3 0.35 -0.7 -0.24-7.1e-3 0.23 0.68 7047 1.0
y2[17] 1.27 4.8e-3 0.43 0.44 0.99 1.27 1.55 2.11 7758 1.0
y2[18] -1.44 4.2e-3 0.37 -2.16 -1.69 -1.43 -1.18 -0.72 8027 1.0
y2[19] 0.85 6.5e-3 0.6 -0.36 0.45 0.85 1.25 2.02 8634 1.0
y2[20] -0.09 5.0e-3 0.44 -0.96 -0.39 -0.1 0.21 0.79 8015 1.0
y2[21] -0.61 4.5e-3 0.39 -1.39 -0.87 -0.61 -0.35 0.15 7565 1.0
y2[22] -0.22 5.3e-3 0.49 -1.16 -0.55 -0.21 0.11 0.74 8376 1.0
y2[23] 0.06 4.4e-3 0.38 -0.69 -0.2 0.06 0.31 0.82 7717 1.0
y2[24] -0.58 4.4e-3 0.4 -1.37 -0.85 -0.58 -0.32 0.21 8164 1.0
y2[25] -0.73 6.3e-3 0.53 -1.77 -1.09 -0.73 -0.39 0.31 7046 1.0
lp__ -14.95 0.24 9.47 -33.92 -21.26 -14.75 -8.62 2.73 1531 1.0
Samples were drawn using NUTS at Tue Nov 3 15:35:02 2020.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
○予測範囲付きy-yプロットで予測と実測を描写
予測の中央値と、実測値の関係をy-yプロットで確認します。また、90%ベイズ信頼区間を算出し、グラフ内にエラーバーとして記載してみました。
$R^2$は94%と、今回の検証ではまずまずの精度のようです。
from sklearn.metrics import r2_score
from scipy.stats import mstats
medY= np.median(fit["y2"], axis=0)
low_y90, high_y90 = mstats.mquantiles(fit["y2"], [0.05, 0.95], axis=0)
low_err = medY - low_y90
high_err = high_y90 - medY
f = r2_score(test[:,-1], medY)
plt.figure(figsize=(5,5))
plt.errorbar(medY, test[:,-1],[low_err, high_err],fmt='ro', capsize=4, ecolor='black')
plt.plot([-5,5], [-5,5], linestyle = '--', color = 'gray')
plt.xlim(-5., 5.)
plt.ylim(-5., 5.)
plt.ylabel("Observed")
plt.xlabel("Predicted")
plt.text(-4.0, 3.5, f'$R^2$ = {f:.3f}\nError bar : 90%', bbox=dict(facecolor='none', edgecolor='black'))
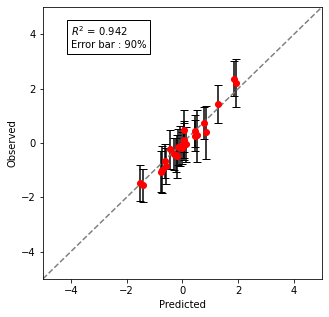
○線形Ridge回帰モデルとの比較
比較として、リーズナブルな予測モデルであるRidge回帰でも予測してみました。
訓練データ、検証データはGPと全く同じデータです。正則化の程度を決めるハイパーパラメータαは1.0としました。
(訓練データが75サンプルと少なめなので、正則化は強めにしましたが、特別な根拠はありません。)
from sklearn import linear_model
ridge = linear_model.Ridge (alpha = 1.) #モデルの定義
ridge.fit(train[:,0:-1], train[:,-1]) #訓練
preY_rid = ridge.predict(test[:,0:-1]) #予測
f = r2_score(test[:,-1], preY_rid)
plt.figure(figsize=(5,5))
plt.scatter(preY_rid, test[:,-1],c='r')
plt.plot([-5,5], [-5,5], linestyle = '--', color = 'gray')
plt.xlim(-5., 5.)
plt.ylim(-5., 5.)
plt.ylabel("Observed")
plt.xlabel("Predicted")
plt.text(-4.0, 4.0, f'$R^2$ = {f:.3f}', bbox=dict(facecolor='none', edgecolor='black'))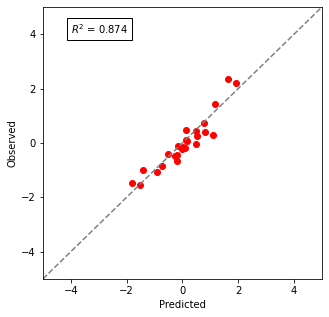
$R^2$は87%でした。GPモデル、Ridge回帰モデルとも簡単に作ったので改善の余地は大いにありますが、GPのほうが予測精度は良さそうですね。
まとめ
今回はStanを使ってガウス過程回帰モデルを実装しました。
ガウス過程は計算コストこそかかりますが、Ridge回帰などと比較して、柔軟かつ精度の高い予測が、少ないデータで可能になります。
今回はボストン住宅価格データに対して特段工夫もなく使いましたが、特徴量を対数などで変換して使う、データに合わせてカーネル関数の設計を変えるなど、改善の余地は大いにあります。
またガウス過程はデータ数が多いと計算量が莫大になるのが弱点ですが、モデルの書き方の工夫や、MCMCではなく変分法を使う方法(こちらはモデルはそのままで、sm.sampling()のところをsm.vb()に変えるだけです。)で改善することも可能です。幅広い用途で使えそうなモデルですので、みなさんも試してみてください。
今回は以上です!

